5187. Point of heights intersection
Find the intersection point
of heights for given triangle.
Input.
The coordinates of the three vertices of triangle (first the coordinates of the
first vertex, then the second, then the third). Coordinates are the pair of
integers not exceeding 104 in absolute value.
Output. Print two numbers – the coordinates of intersection point for triangle
heights with an accuracy of at least 6 decimal digits.
|
Sample input |
Sample output |
|
0 0 3 0 0 4 |
0.0 0.0 |
SOLUTION
geometry
Algorithm analysis
Let A(xa, ya), B(xb,
yb), C(xc, yc) be three triangle vertices. Draw the heights AK and BL. The point of their intersection H will be the desired
one.
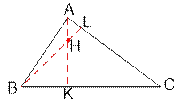
Write the
equation of the line AK: it must pass through the vertex A and be perpendicular
to the line BC. Let the equation of the line AK have the form a1x + b1y = c1. Then
the vector (a1, b1) coincides with the direction of the vector BC and we
can put (a1, b1) = (xc – xb,
yc – yb). Equation of the line AK has the form
(xc – xb)x + (yc
– yb)y = c1
Since line AK
passes through point A, substituting the coordinates of point A(xa, ya) into its equation, we find the value of c1:
(xc
– xb) xa + (yc
– yb) ya = c1
Similarly find
the equation of the line BL. Let it has the form a2x + b2y = c2. The
vector (a2, b2) coincides with the direction of the vector AC and we
can put (a2, b2) = (xc
– xa, yc – ya).
Point B lies on line BL, hence
(xc
– xa) xb + (yc
– ya) yb = c2
The intersection
point of the heights of triangle can be found by solving the system of
equations
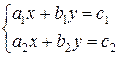
with Kramer’s method.
Algorithm realization
Function kramer finds the solution (x,
y) of system of equations
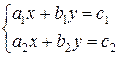
void kramer(double a1, double b1, double c1,
double a2, double b2, double c2, double &x, double &y)
{
double d = a1 * b2 - a2 * b1;
double dx = c1 * b2 - c2 * b1;
double dy = a1 * c2 - a2 * c1;
x = dx / d; y = dy / d;
}
Read the input data.
scanf("%lf %lf %lf %lf %lf %lf",&xa,&ya,&xb,&yb,&xc,&yc);
Find
the equation of the line AK:
a1x + b1y = c1.
a1 = xc - xb;
b1 = yc - yb;
c1 = xa * (xc -
xb) + ya * (yc - yb);
Find
the equation of the line BL:
a2x + b2y = c2.
a2 = xc - xa;
b2 = yc - ya;
c2 = xb * (xc -
xa) + yb * (yc - ya);
Find and print the intersection point of the triangle heights.
kramer(a1,b1,c1,a2,b2,c2,x,y);
printf("%.6lf %.6lf\n",x,y);
Java
realization
import java.util.*;
public class Main
{
static double[] kramer(double a1, double b1, double c1,
double a2, double b2, double c2)
{
double res[] = new double[2]; // x, y
double d = a1 * b2 - a2 * b1;
double dx = c1 * b2 - c2 * b1;
double dy = a1 * c2 - a2 * c1;
res[0] = dx / d;
res[1] = dy / d;
return res;
}
public static void main(String []args)
{
Scanner con = new Scanner(System.in);
double xa = con.nextDouble();
double ya = con.nextDouble();
double xb = con.nextDouble();
double yb = con.nextDouble();
double xc = con.nextDouble();
double yc = con.nextDouble();
double a1 = xc - xb;
double b1 = yc - yb;
double c1 = xa * (xc - xb) + ya * (yc - yb);
double a2 = xc - xa;
double b2 = yc - ya;
double c2 = xb * (xc - xa) + yb * (yc - ya);
double res[] = kramer(a1,b1,c1,a2,b2,c2);
System.out.println(res[0] + " " + res[1]);
con.close();
}
}